
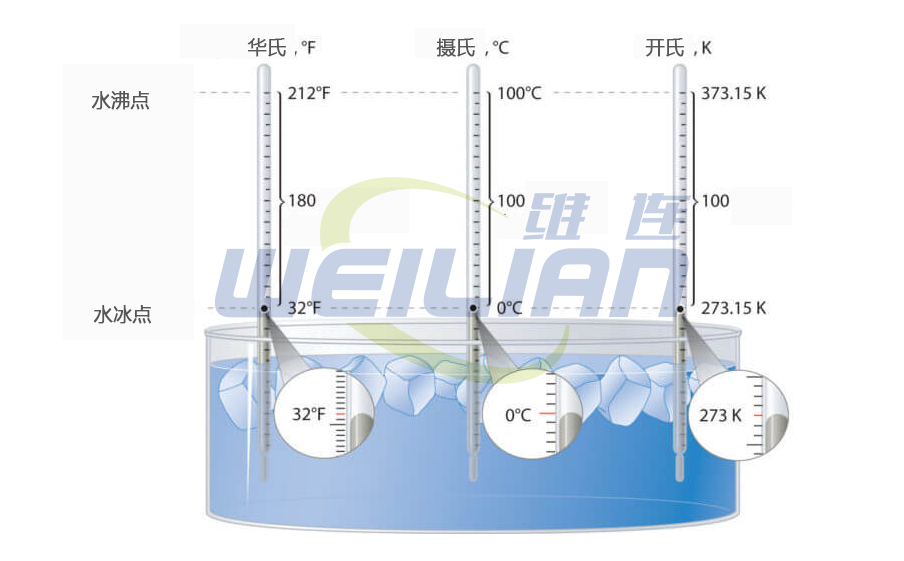
 温标之间的关系 温标之间的关系
温标之间的关系 温标之间的关系
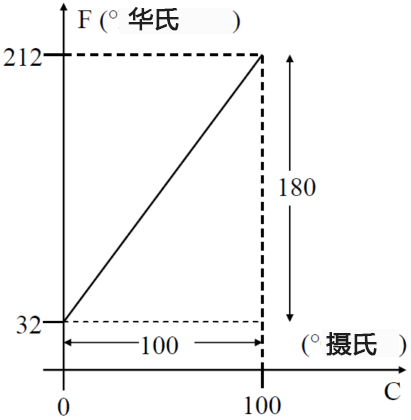
General equation using straight lines:
y = mx + cUsing the general straight line equation and the above figure, the following equation is obtained
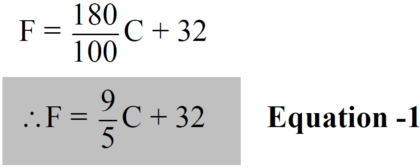
Now we can also use Fahrenheit to express Celsius. From Eq. - 1:
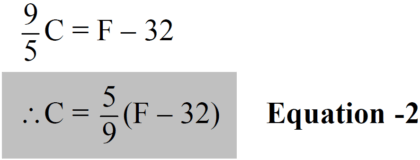
Now we have solved the basic formula for converting degrees Celsius to degrees Fahrenheit or vice versa. Using the same process as above, we can also calculate the relationship between different temperature scales.
Fast transition between temperatures: Celsius to Fahrenheit: multiply the temperature by 2, then add 30 degrees Fahrenheit to Celsius: subtract 30 from the temperature. Then divide by 2 Kelvin to Fahrenheit: subtract 273.15, multiply by 1.8, and then add 32 Fahrenheit to Kelvin: subtract 32, multiply by 5, divide by 9, and then add 273.15 Kelvin to Celsius: add 273 Celsius to Kelvin: subtract 273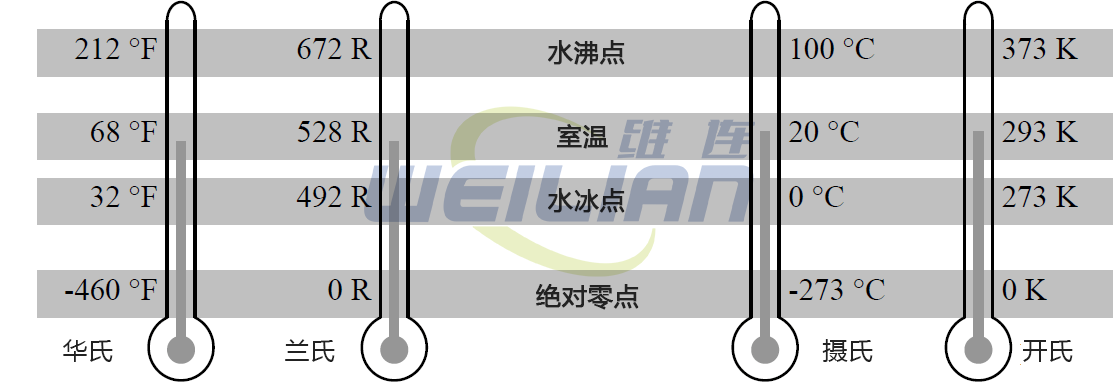
Example - 1
Convert the absolute zero value of the temperature (– 273.15 ° C) to Fahrenheit.
F = (9/5)C + 32 = (9/5)×(-273.15) + 32 = -459.67 °F ≈ -460 °F
Example - 2
Convert 86 ° F to Celsius, Rankine, and Kelvin.
C = (5/9)(F – 32) = (5/9)×(86 – 32) = 30 °C
R = F + 460 = 86 + 460 = 546 R
K = C + 273 = 30 + 273 = 303 K
Example - 3
Determines the temperature in degrees Fahrenheit, which will be converted to the same value in degrees Celsius.
In Formula - 2 (or Formula - 1), set C=F:
F = (5/9)(F – 32) ⇒ 9F = 5F – 160 ⇒ 4F = -160 ⇒ F = -40 °F
Example - 4
Convert 0 ° F to Celsius.
C = (5/9)(F – 32) = (5/9)(0 – 32) = -17.78 °C

